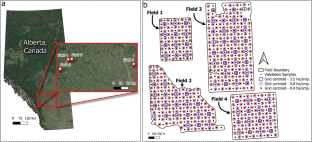
Given the high costs of soil sampling, low and extra-low sampling densities are still being used. Low-density soil sampling usually does not allow the computation of experimental variograms reliable enough to fit models and perform interpolation. In the absence of geostatistical tools, deterministic methods such as inverse distance weighting (IDW) are recommended but they are susceptible to the “bull’s eye” effect, which creates non-smooth surfaces. This study aims to develop and assess interpolation methods or approaches to produce soil test maps that are robust and maximize the information value contained in sparse soil sampling data. Eleven interpolation procedures, including traditional methods, a newly proposed methodology, and a kriging-based approach, were evaluated using grid soil samples from four fields located in Central Alberta, Canada. In addition to the original 0.4 ha⋅sample−1 sampling scheme, two sampling design densities of 0.8 and 3.5 ha⋅sample−1 were considered. Among the many outcomes of this study, it was found that the field average never emerged as the basis for the best approach. Also, none of the evaluated interpolation procedures appeared to be the best across all fields, soil properties, and sampling densities. In terms of robustness, the proposed kriging-based approach, in which the nugget effect estimate is set to the value of the semi-variance at the smallest sampling distance, and the sill estimate to the sample variance, and the IDW with the power parameter value of 1.0 provided the best approaches as they rarely yielded errors worse than those obtained with the field average.