Flow modeling and structural characterization in fungal pellets

Abstract

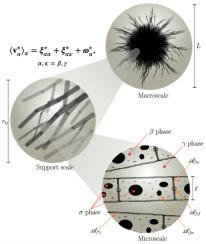
Fungal pellets are hierarchical systems that can be found in an ample variety of applications. Modeling transport phenomena in this type of systems is a challenging but necessary task to provide knowledge-based processes that improve the outcome of their biotechnological applications. In this work, an upscaled model for total mass and momentum transport in fungal pellets is implemented and analyzed, using elements of the volume averaging and adjoint homogenization methods departing from the governing equations at the microscale in the intracellular and extracellular phases. The biomass is assumed to be composed of a non-Newtonian fluid and the organelles impervious to momentum transport are modeled as a rigid solid phase. The upscaled equations contain effective-medium coefficients, which are predicted from the solution of adjoint closure problems in a three-dimensional periodic domains representative of the microstructure. The construction of these domains was performed for Laccaria trichodermophora based on observations of actual biological structures. The upscaled model was validated with direct numerical simulations in homogeneous portions of the pellets core. It is shown that no significant differences are observed when the dolipores are open or closed to fluid flow. By comparing the predictions of the average velocity in the extracellular phase resulting from the upscaled model with those from the classical Darcy equation (i.e., assuming that the biomass is a solid phase) the contribution of the intracellular fluid phase was evidenced. This work sets the foundations for further studies dedicated to transport phenomena in this type of systems.