Extension of Prandtl’s solution to a general isotropic model of plasticity including internal variables

Abstract

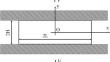
This paper presents a semi-analytic solution for the continued quasi-static compression of a thin rigid/plastic layer between two rigid, parallel rough plates. The constitutive equations of isotropic material postulate that the shear yield stress depends on the equivalent strain rate, the equivalent strain, and other internal variables. No restriction is imposed on this dependence. The general solution is valid for any finite number of internal variables. This solution reduces to several simple differential equations and one transcendental equation in Lagrangian coordinates. The solution is based on the standard assumptions in formulating the boundary value problem for simpler material models. More straightforward particular cases of the constitutive equations that are important for applications are considered separately. The solution reduces to a single differential equation in the most straightforward cases. A transcendental equation should be solved to find the initial condition of this differential equation. The friction factor’s effect on the solution’s qualitative behavior is discussed in detail. A numerical example illustrates the solution for an uncoupled material model. An applied aspect of this research is that its results can be used to analyze the plane-strain compression of thin metal strips, an essential metal-forming process.