The Emmons Problem Revisited

Abstract

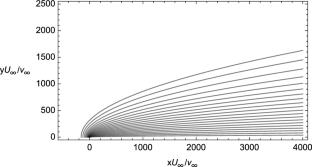
The “Emmons Problem” is a foundation of fire science and gives a mathematical boundary layer solution to the burning of a vaporizing fuel from the surface of a flat plate immersed in a uniform flow of oxidizing gas. It approximates the Navier–Stokes equations assuming infinitely fast chemistry and ignores differential diffusion and thermal radiation. This allows “similarity” solutions to be developed and expressed in terms of the classic Blasius function. The current paper extends the solution, in mathematical form, to the entire domain far from the boundary layer and upstream of the leading edge. The introduction of conformal parabolic coordinates and use of the Howarth transformation allows the solution for the stream function to be expressed in exactly the same form as that found by Emmons and furnishes an explicit recipe for the pressure perturbation. The same coordinate transformations allow the exact solution of the full elliptic mixture fraction equation to be obtained, and the representation of the velocity components in terms of the stream function guarantees that the continuity equation is also satisfied exactly. Further, an exact solution to the transverse momentum equation is also displayed permitting the introduction of a crossflow into the spectrum of results obtained. In short, an analytic solution is found for the Emmons problem in the entire elliptic domain - upstream and in the far field.