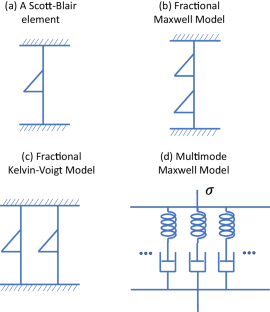
In this work, we investigate the large amplitude oscillatory shear (LAOS) behavior of white-wheat, wholegrain-wheat and chickpea flour doughs experimentally and theoretically. In order to accurately model the LAOS behavior of those doughs, it was important to study their linear viscoelastic as well as stress relaxation behaviors. We analyzed the linear viscoelastic behavior theoretically through the single spring-pot model, the fractional Maxwell model (FMM) and the fractional Kelvin-Voigt model. We found that the FMM is best suited to describe the LVE of the doughs we investigated. The damping function form was chosen based on stress relaxation and strain sweep experiments. We found that the Soskey-Winter (SW) equation is suitable for accurately describing the damping behavior of doughs. The LAOS experimental results were obtained at a set of strain amplitude and frequency values to build the Lissajous-Bowditch curves in Pipkin space. We modeled the LAOS stress response using the Kay-Bernstein Kearsley and Zapas (K-BKZ) model coupled with the FMM and SW models. The SW parameters were optimized for each dough by fitting the LAOS Lissajous-Bowditch curves in Pipkin space. The obtained fits to LAOS stress response were very good and illustrate that the FMM-SW-K-BKZ model provides an excellent description of the LAOS behavior of the different variety of doughs examined in this work. Moreover, the study shows that LAOS Lissajous-Bowditch curves provide characteristically different shapes for wheat and chickpea flour doughs.