Low-rank Representation for Seismic Reflectivity and its Applications in Least-squares Imaging

Abstract

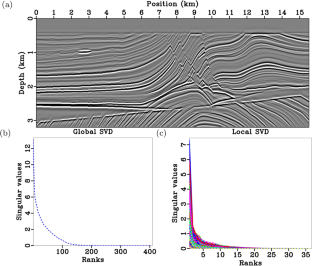
Sparse representation and inversion have been widely used in the acquisition and processing of geophysical data. In particular, the low-rank representation of seismic signals shows that they can be determined by a few elementary modes with predominantly large singular values. We review global and local low-rank representation for seismic reflectivity models and then apply it to least-squares migration (LSM) in acoustic and viscoacoustic media. In the global singular value decomposition (SVD), the elementary modes determined by singular vectors represent horizontal and vertical stratigraphic segments sorted from low to high wavenumbers, and the corresponding singular values reflect the contribution of these basic modes to form a broadband reflectivity model. In contrast, local SVD for grouped patch matrices can capture nonlocal similarity and thus accurately represent the reflectivity model with fewer ranks than the global SVD method. Taking advantage of this favorable sparsity, we introduce a local low-rank regularization into LSM to estimate subsurface reflectivity models. A two-step algorithm is developed to solve this low-rank constrained inverse problem: the first step is for least-squares data fitting and the second is for weighted nuclear-norm minimization. Numerical experiments for synthetic and field data demonstrate that the low-rank constraint outperforms conventional shaping and total-variation regularizations, and can produce high-quality reflectivity images for complicated structures and low signal-to-noise data.