Smooth Transonic Flows with Nonzero Vorticity to a Quasi Two Dimensional Steady Euler Flow Model

Abstract

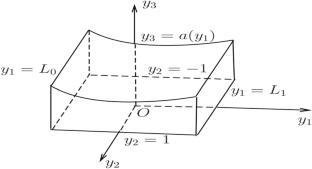
This paper concerns smooth transonic flows with nonzero vorticity in De Laval nozzles for a quasi two dimensional steady Euler flow model which is a generalization of the classical quasi one dimensional model. First we examine the existence and uniqueness of smooth transonic flows to the quasi one-dimensional model, which start from a subsonic state at the entrance and accelerate to reach a sonic state at the throat and then become supersonic are proved by a reduction of degeneracy of the velocity near the sonic point and the implicit function theorem. These flows can have positive or zero acceleration at their sonic points and the degeneracy types near the sonic point are classified precisely. We then establish the structural stability of the smooth one dimensional transonic flow with positive acceleration at the sonic point for the quasi two dimensional steady Euler flow model under small perturbations of suitable boundary conditions, which yields the existence and uniqueness of a class of smooth transonic flows with nonzero vorticity and positive acceleration to the quasi two dimensional model. The positive acceleration of the one dimensional transonic solutions plays an important role in searching for an appropriate multiplier for the linearized second order mixed type equations. A deformation-curl decomposition for the quasi two dimensional model is utilized to deal with the transonic flows with nonzero vorticity.