Finite-element approximation for three-dimensional nanofluid flow with heat transfer over a non-linearly stretching sheet

Abstract

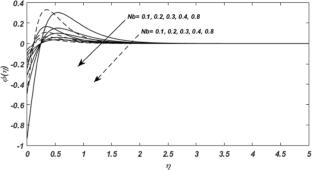
This article uses a finite-element approximation approach for solving a three-dimensional flow problem of a nanofluid influenced by heat transfer due to nanoparticles over a non-linearly stretching sheet within an unbounded domain. Utilising similarity transformations, a well-posed coupled system of nonlinear ordinary differential equations is derived from the governing partial differential equations describing the flow and heat transfer processes. The resulting system is then solved by using quadratic Lagrange polynomials as basic functions over a mesh of different finite elements through the Galerkin finite element (GFE) technique. This implementation is based on a regular grid utilising Lagrange polynomials for solving the converted equations. The effects of various parameters of interest are efficiently discussed with the help of graphs and numeric tables. Both numerical and exact solutions are compared favourably, demonstrating a high level of accuracy. It is noteworthy that the GFE method emerges as a much more stable numerical technique than the other existing analytic and semi-analytical methods. Furthermore, the adopted finite-element method reduces the dimensionality of Sobolev's space's finite-dimensional subspace and also improves the solution's convergence rate. Moreover, the velocity is negative, and its magnitude increases as the stretching rates ratio increases due to the downward flow in the vertical direction. The temperature and heat transmission from the sheet are barely impacted by Brownian motion due to the dominance of other forces and length scales involved in the heat transfer process.