Estimation of \( P[Y Q1 Decision Sciences Annals of Data Science Pub Date : 2023-08-17 DOI:10.1007/s40745-023-00487-z Dipak D. Patil, U. V. Naik-Nimbalkar, M. M. Kale

Abstract

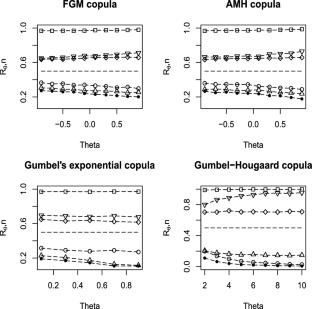
The stress–strength model is a basic tool used in evaluating the reliability \( R = P(Y < X)\). We consider an expression for R where the random variables X and Y denote strength and stress, respectively. The system fails only if the stress exceeds the strength. We aim to study the effect of the dependency between X and Y on R. We assume that X and Y follow Weibull distributions and their dependency is modeled by a copula with the dependency parameter \( \theta \). We compute R for Farlie–Gumbel–Morgenstern (FGM), Ali–Mikhail–Haq (AMH), Gumbel’s bivariate exponential copulas, and for Gumbel–Hougaard (GH) copula using a Monte-Carlo integration technique. We plot the graph of R versus \(\theta \) to study the effect of dependency on R. We estimate R by plugging in the estimates of the marginal parameters and of \( \theta \) in its expression. The estimates of the marginal parameters are based on the marginal likelihood. The estimates of \(\theta \) are obtained from two different methods; one is based on the conditional likelihood and the other is based on the method of moments using Blomqvist’s beta. Asymptotic distribution of both the estimators of R is obtained. Finally, analysis of real data set is also performed for illustrative purposes.