The Knuth–Morris–Pratt (KMP) algorithm for string search is notoriously difficult to understand. Lost in a sea of index arithmetic, most explanations of KMP obscure its essence. This paper constructs KMP incrementally, using pictures to illustrate each step. The end result is easier to comprehend. Additionally, the derivation uses only elementary functional programming techniques.
Behavioral software contracts allow programmers to strengthen the obligations and promises that they express with conventional types. They lack expressive power, though, when it comes to invariants that hold across several function calls. Trace contracts narrow this expressiveness gap. A trace contract is a predicate over the sequence of values that flow through function calls and returns. This paper presents a principled design, an implementation, and an evaluation of trace contracts.
The other day, I was assembling lecture material for a course on Agda. Pursuing an application-driven approach, I was looking for correctness proofs of popular algorithms. One of my all-time favourites is Huffman data compression (Huffman, 1952). Even though it is probably safe to assume that you are familiar with this algorithmic gem, a brief reminder of the essential idea may not be amiss.
This paper describes a purely functional library for computing level-p-complexity of Boolean functions and applies it to two-level iterated majority. Boolean functions are simply functions from n bits to one bit, and they can describe digital circuits, voting systems, etc. An example of a Boolean function is majority, which returns the value that has majority among the n input bits for odd n. The complexity of a Boolean function f measures the cost of evaluating it: how many bits of the input are needed to be certain about the result of f. There are many competing complexity measures, but we focus on level-p-complexity — a function of the probability p that a bit is 1. The level-p-complexity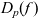 
$D_p(f)$ is the minimum expected cost when the input bits are independent and identically distributed with Bernoulli(p) distribution. We specify the problem as choosing the minimum expected cost of all possible decision trees — which directly translates to a clearly correct, but very inefficient implementation. The library uses thinning and memoization for efficiency and type classes for separation of concerns. The complexity is represented using (sets of) polynomials, and the order relation used for thinning is implemented using polynomial factorization and root counting. Finally, we compute the complexity for two-level iterated majority and improve on an earlier result by J. Jansson.
京公网安备 11010802042870号
京ICP备2023020795号-1
扫码关注我们
求助内容：
应助结果提醒方式：