We describe the one-generator braces A satisfying the condition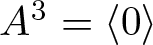 
$A^3 = langle 0 rangle$.
We prove that there exists an algorithm for determining whether two piecewise-linear spatial graphs are isomorphic. In its most general form, our theorem applies to spatial graphs furnished with vertex colourings, edge colourings and/or edge orientations.
We first show that spatial graphs admit canonical decompositions into blocks, that is, spatial graphs that are non-split and have no cut vertices, in a suitable topological sense. Then, we apply a result of Haken and Matveev in order to algorithmically distinguish these blocks.
We construct and study the moduli of stable hypersurfaces in toric orbifolds. Let X be a projective toric orbifold and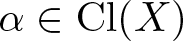 
$alpha in operatorname{Cl}(X)$ an ample class. The moduli space is constructed as a quotient of the linear system 
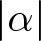$|alpha|$ by 
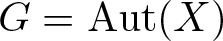$G = operatorname{Aut}(X)$. Since the group G is non-reductive in general, we use new techniques of non-reductive geometric invariant theory. Using the A-discriminant of Gelfand, Kapranov and Zelevinsky, we prove semistability for quasismooth hypersurfaces of toric orbifolds. Further, we prove the existence of a quasi-projective moduli space of quasismooth hypersurfaces in a weighted projective space when the weighted projective space satisfies a certain condition. We also discuss how to proceed when this condition is not satisfied. We prove that the automorphism group of a quasismooth hypersurface of weighted projective space is finite excluding some low degrees.
In this note, we establish a boundary maximum principle for a class of stationary pairs of varifolds satisfying a fixed contact angle condition in any compact Riemannian manifold with smooth boundary.
We show that if an open set in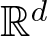 
$mathbb{R}^d$ can be fibered by unit n-spheres, then 
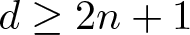$d geq 2n+1$, and if 
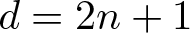$d = 2n+1$, then the spheres must be pairwise linked, and 
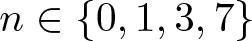$n in left{0, 1, 3, 7 right}$. For these values of n, we construct unit n-sphere fibrations in 
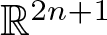$mathbb{R}^{2n+1}$.
We consider the broadest concept of the gradient Yamabe soliton, the conformal gradient soliton. In this paper, we elucidate the structure of complete gradient conformal solitons under some assumption, and provide some applications to gradient Yamabe solitons. These results enhance the understanding gained from previous research. Furthermore, we give an affirmative partial answer to the Yamabe soliton version of Perelman’s conjecture.
In this paper, we mainly prove the following conjectures of Sun [16]: Let p > 3 be a prime. Then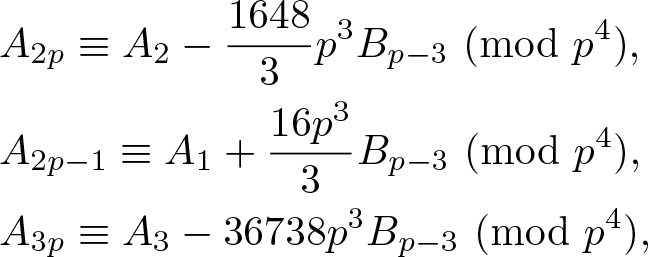
begin{align*}&A_{2p}equiv A_2-frac{1648}3p^3B_{p-3} ({rm{mod}} p^4),&A_{2p-1}equiv A_1+frac{16p^3}3B_{p-3} ({rm{mod}} p^4),&A_{3p}equiv A_3-36738p^3B_{p-3} ({rm{mod}} p^4),end{align*}
where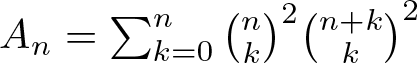 
$A_n=sum_{k=0}^nbinom{n}k^2binom{n+k}{k}^2$ is the nth Apéry number, and Bn is the nth Bernoulli number.
京公网安备 11010802042870号
京ICP备2023020795号-1
扫码关注我们
求助内容：
应助结果提醒方式：