In this work, we consider two sets of dependent variables 
${X_{1},ldots,X_{n}}$ and 
${Y_{1},ldots,Y_{n}}$, where 
$X_{i}sim EW(alpha_{i},lambda_{i},k_{i})$ and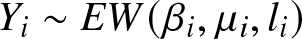 
$Y_{i}sim EW(beta_{i},mu_{i},l_{i})$, for 
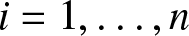$i=1,ldots, n$, which are coupled by Archimedean copulas having different generators. We then establish different inequalities between two extremes, namely, 
$X_{1:n}$ and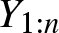 
$Y_{1:n}$ and 
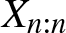$X_{n:n}$ and 
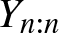$Y_{n:n}$, in terms of the usual stochastic, star, Lorenz, hazard rate, reversed hazar
We focus on exponential semi-Markov decision processes with unbounded transition rates. We first provide several sufficient conditions under which the value iteration procedure converges to the optimal value function and optimal deterministic stationary policies exist. These conditions are also valid for general semi-Markov decision processes possibly with accumulation points. Then, we apply our results to a service rate control problem with impatient customers. The resulting exponential semi-Markov decision process has unbounded transition rates, which makes the well-known uniformization technique inapplicable. We analyze the structure of the optimal policy and the monotonicity of the optimal value function by using the customization technique that was introduced by the author in prior work.
In this paper, the ordering properties of convex and increasing convex orders of the dependent random variables are studied. Some closure properties of the convex and increasing convex orders under independent random variables are extended to the dependent random variables under the Archimedean copula. Two applications are provided to illustrate our results.
We consider the propagation of a stochastic SIR-type epidemic in two connected populations: a relatively small local population of interest which is surrounded by a much larger external population. External infectives can temporarily enter the small population and contribute to the spread of the infection inside this population. The rules for entry of infectives into the small population as well as their length of stay are modeled by a general Markov queueing system. Our main objective is to determine the distribution of the total number of infections within both populations. To do this, the approach we propose consists of deriving a family of martingales for the joint epidemic processes and applying classical stopping time or convergence theorems. The study then focuses on several particular cases where the external infection is described by a linear branching process and the entry of external infectives obeys certain specific rules. Some of the results obtained are illustrated by numerical examples.
京公网安备 11010802042870号
京ICP备2023020795号-1
扫码关注我们
求助内容：
应助结果提醒方式：