Given a perfect field 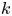 $k$ with algebraic closure
$k$ with algebraic closure 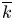 $overline {k}$ and a variety
$overline {k}$ and a variety 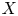 $X$ over
$X$ over 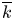 $overline {k}$, the field of moduli of
$overline {k}$, the field of moduli of 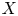 $X$ is the subfield of
$X$ is the subfield of 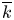 $overline {k}$ of elements fixed by field automorphisms
$overline {k}$ of elements fixed by field automorphisms 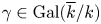 $gamma in operatorname {Gal}(overline {k}/k)$ such that the Galois conjugate
$gamma in operatorname {Gal}(overline {k}/k)$ such that the Galois conjugate 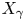 $X_{gamma }$ is isomorphic to
$X_{gamma }$ is isomorphic to 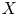 $X$. The field of moduli is contained in all subextensions
$X$. The field of moduli is contained in all subextensions 
In this paper, we present a solution to the problem of the analytic classification of germs of plane curves with several irreducible components. Our algebraic approach follows precursive ideas of Oscar Zariski and as a subproduct allows us to recover some particular cases found in the literature.
The aim of the present paper is to derive effective discrepancy estimates for the distribution of rational points on general semisimple algebraic group varieties, in general families of subsets and at arbitrarily small scales. We establish mean-square, almost sure and uniform estimates for the discrepancy with explicit error bounds. We also prove an analogue of W. Schmidt's theorem, which establishes effective almost sure asymptotic counting of rational solutions to Diophantine inequalities in the Euclidean space. We formulate and prove a version of it for rational points on the group variety, with an effective bound which in some instances can be expected to be the best possible.
We prove that the multiplicity of a filtration of a local ring satisfies various convexity properties. In particular, we show the multiplicity is convex along geodesics. As a consequence, we prove that the volume of a valuation is log convex on simplices of quasi-monomial valuations and give a new proof of a theorem of Xu and Zhuang on the uniqueness of normalized volume minimizers. In another direction, we generalize a theorem of Rees on multiplicities of ideals to filtrations and characterize when the Minkowski inequality for filtrations is an equality under mild assumptions.
We show that for every finite set of prime numbers  $S$, there are at most finitely many singular moduli that are
$S$, there are at most finitely many singular moduli that are  $S$-units. The key new ingredient is that for every prime number
$S$-units. The key new ingredient is that for every prime number  $p$, singular moduli are
$p$, singular moduli are  $p$-adically disperse. We prove analogous results for the Weber modular functions, the
$p$-adically disperse. We prove analogous results for the Weber modular functions, the  $lambda$-invariants and the McKay–Thompson series associated with the elements of the monster group. Finally, we also obtain that a modular function that specializes to infinitely many algebraic units at quadratic imaginary numbers must be a weak modular unit.
$lambda$-invariants and the McKay–Thompson series associated with the elements of the monster group. Finally, we also obtain that a modular function that specializes to infinitely many algebraic units at quadratic imaginary numbers must be a weak modular unit.
We prove the Hasse principle for a smooth projective variety  $Xsubset mathbb {P}^{n-1}_mathbb {Q}$ defined by a system of two cubic forms
$Xsubset mathbb {P}^{n-1}_mathbb {Q}$ defined by a system of two cubic forms  $F,G$ as long as
$F,G$ as long as  $ngeq 39$. The main tool here is the development of a version of Kloosterman refinement for a smooth system of equations defined over
$ngeq 39$. The main tool here is the development of a version of Kloosterman refinement for a smooth system of equations defined over  $mathbb {Q}$.
$mathbb {Q}$.
The straightening–unstraightening correspondence of Grothendieck–Lurie provides an equivalence between cocartesian fibrations between  $(infty, 1)$-categories and diagrams of
$(infty, 1)$-categories and diagrams of  $(infty, 1)$-categories. We provide an alternative proof of this correspondence, as well as an extension of straightening–unstraightening to all higher categorical dimensions. This is based on an explicit combinatorial result relating two types of fibrations between double categories, which can be applied inductively to construct the straightening of a cocartesian fibration between higher categories.
$(infty, 1)$-categories. We provide an alternative proof of this correspondence, as well as an extension of straightening–unstraightening to all higher categorical dimensions. This is based on an explicit combinatorial result relating two types of fibrations between double categories, which can be applied inductively to construct the straightening of a cocartesian fibration between higher categories.

