Collisionless shocks are frequently analysed using the magnetohydrodynamics (MHD) formalism, even though MHD assumes a small mean free path. Yet, isotropy of pressure, the fruit of binary collisions and assumed in MHD, may not apply in collisionless shocks. This is especially true within a magnetized plasma, where the field can stabilize an anisotropy. In a previous article (Bret & Narayan, J. Plasma Phys., vol. 88, no. 6, 2022b, p. 905880615), a model was presented capable of dealing with the anisotropies that may arise at the front crossing. It was solved for any orientation of the field with respect to the shock front. Yet, for some values of the upstream parameters, several downstream solutions were found. Here, we complete the work started in Bret & Narayan (J. Plasma Phys., vol. 88, no. 6, 2022b, p. 905880615) by showing how to pick the physical solution out of the ones offered by the algebra. This is achieved by 2 means: (i) selecting the solution that has the downstream field obliquity closest to the upstream one. This criterion is exemplified on the parallel case and backed up by particle-in-cell simulations. (ii) Filtering out solutions which do not satisfy a criteria already invoked to trim multiple solutions in MHD: the evolutionarity criterion, that we assume valid in the collisionless case. The end result is a model in which a given upstream configuration results in a unique, or no downstream configuration (as in MHD). The largest departure from MHD is found for the case of a parallel shock.
The Okubo–Weiss (Okubo, Deep-Sea Res., vol. 17, issue 3, 1970, pp. 445–454; Weiss, Physica D, vol. 48, issue 2, 1991, pp. 273–294) criterion has been widely used as a diagnostic tool to divide a two-dimensional (2-D) hydrodynamical flow field into hyperbolic and elliptic regions. This paper considers extension of these ideas to 2-D magnetohydrodynamic (MHD) flows, and presents an Okubo–Weiss-type criterion to parameterize the magnetic field topology in 2-D MHD flows. This ensues via its topological connections with the intrinsic metric properties of the underlying magnetic flux manifold, and is illustrated by recasting the Okubo–Weiss-type criterion via the 2-D MHD stationary generalized Alfvénic state condition to approximate the slow-flow-variation ansatz imposed in its derivation. The Okubo–Weiss-type parameter then turns out to be related to the sign definiteness of the Gaussian curvature of the magnetic flux manifold. A similar formulation becomes possible for 2-D electron MHD flows, by using the generalized magnetic flux framework to incorporate the electron-inertia effects. Numerical simulations of quasi-stationary vortices in 2-D MHD flows in the decaying turbulence regime are then given to demonstrate that the Okubo–Weiss-type criterion is able to separate the MHD flow field into elliptic and hyperbolic field configurations very well.
Some stellarators tend to benefit from favourable average magnetic curvature for trapped particles when the plasma pressure is sufficiently high. This so-called maximum-$J$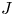
property has several positive implications, such as good fast-particle confinement, magnetohydrodynamic stability and suppression of certain trapped-particle instabilities. This property cannot be attained in quasisymmetric stellarators, in which deeply trapped particles experience average bad curvature and therefore precess in the diamagnetic direction close to the magnetic axis. However, quasi-isodynamic stellarators offer greater flexibility and allow the average curvature to be favourable and the precession to be reversed. We find that it is possible to design such stellarators so that the maximum-$J$
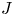condition is satisfied for the great majority of all particles, even when the plasma pressure vanishes. The qualitative properties of such a stellarator field can be derived analytically by examining the most deeply and the most shallowly trapped particles, although some small fraction of the latter will inevitably not behave as desired. However, through numerical optimisation, we construct a vacuum field in which 99.6 % of all trapped particles satisfy the maximum-$J$
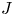condition.
京公网安备 11010802042870号
京ICP备2023020795号-1
扫码关注我们
求助内容：
应助结果提醒方式：