Proceedings of the Royal Society of Edinburgh Section A-Mathematics最新文献

We prove that any positive rational number is the sum of distinct unit fractions with denominators in ${p-1 : ptextrm { prime}}$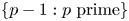. The same conclusion holds for the set ${p-h : ptextrm { prime}}$ 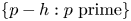for any $hin mathbb {Z}backslash {0}$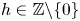, provided a necessary congruence condition is satisfied. We also prove that this is true for any subset of the primes of relative positive density, provided a necessary congruence condition is satisfied.

For an action of a finite group on a finite EI quiver, we construct its ‘orbifold’ quotient EI quiver. The free EI category associated to the quotient EI quiver is equivalent to the skew group category with respect to the given group action. Specializing the result to a finite group action on a finite acyclic quiver, we prove that, under reasonable conditions, the skew group category of the path category is equivalent to a finite EI category of Cartan type. If the ground field is of characteristic $p$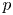 and the acting group is a cyclic $p$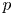-group, we prove that the skew group algebra of the path algebra is Morita equivalent to the algebra associated to a Cartan matrix, defined in [C. Geiss, B. Leclerc, and J. Schröer, Quivers with relations for symmetrizable Cartan matrices I: Foundations, Invent. Math. 209 (2017), 61–158]. We apply the Morita equivalence to construct a categorification of the folding projection between the root lattices with respect to a graph automorphism. In the Dynkin cases, the restriction of the categorification to indecomposable modules corresponds to the folding of positive roots.

This article is concerned with the problem of determining an unknown source of non-potential, external time-dependent perturbations of an incompressible fluid from large-scale observations on the flow field. A relaxation-based approach is proposed for accomplishing this, which makes use of a nonlinear property of the equations of motions to asymptotically enslave small scales to large scales. In particular, an algorithm is introduced that systematically produces approximations of the flow field on the unobserved scales in order to generate an approximation to the unknown force; the process is then repeated to generate an improved approximation of the unobserved scales, and so on. A mathematical proof of convergence of this algorithm is established in the context of the two-dimensional Navier–Stokes equations with periodic boundary conditions under the assumption that the force belongs to the observational subspace of phase space; at each stage in the algorithm, it is shown that the model error, represented as the difference between the approximating and true force, asymptotically decreases to zero in a geometric fashion provided that sufficiently many scales are observed and certain parameters of the algorithm are appropriately tuned.

We study tropical line arrangements associated to a three-regular graph $G$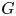 that we refer to as tropical graph curves. Roughly speaking, the tropical graph curve associated to $G$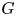, whose genus is $g$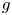, is an arrangement of $2g-2$ lines in tropical projective space that contains $G$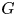 (more precisely, the topological space associated to $G$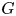) as a deformation retract. We show the existence of tropical graph curves when the underlying graph is a three-regular, three-vertex-connected planar graph. Our method involves explicitly constructing an arrangement of lines in projective space, i.e. a graph curve whose tropicalization yields the corresponding tropical graph curve and in this case, solves a topological version of the tropical lifting problem associated to canonically embedded graph curves. We also show that the set of tropical graph curves that we construct are connected via certain local operations. These local operations are inspired by Steinitz’ theorem in polytope theory.

We determine when the integral homology of the classifying space of a $PU(n)$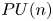-gauge group over the sphere $S^2$ 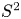has torsion.