We generalize the known collision results for a solid in a 3D compressible Newtonian fluid to compressible non-Newtonian ones, and to Newtonian fluids with temperature-depending viscosities.
In this paper, we consider the following non-linear system involving the fractional Laplacian0.1begin{equation} left{begin{array}{@{}ll} (-Delta)^{s} u (x)= f(u,,v), (-Delta)^{s} v (x)= g(u,,v), end{array} right. end{equation}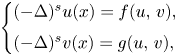 in two different types of domains, one is bounded, and the other is an infinite cylinder, where $0< s<1$
in two different types of domains, one is bounded, and the other is an infinite cylinder, where $0< s<1$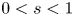 . We employ the direct sliding method for fractional Laplacian, different from the conventional extension and moving planes methods, to derive the monotonicity of solutions for (0.1) in $x_n$
. We employ the direct sliding method for fractional Laplacian, different from the conventional extension and moving planes methods, to derive the monotonicity of solutions for (0.1) in $x_n$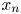 variable. Meanwhile, we develop a new iteration method for systems in the proofs. Hopefully, the iteration method can also be applied to solve other problems.
variable. Meanwhile, we develop a new iteration method for systems in the proofs. Hopefully, the iteration method can also be applied to solve other problems.
In this paper, we review some recent results on nonlocal interaction problems. The focus is on interaction kernels that are anisotropic variants of the classical Coulomb kernel. In other words, while preserving the same singularity at zero of the Coulomb kernel, they present preferred directions of interaction. For kernels of this kind and general confinement we will prove existence and uniqueness of minimizers of the corresponding energy. In the case of a quadratic confinement we will review a recent result by Carrillo and Shu about the explicit characterization of minimizers, and present a new proof, which has the advantage of being extendable to higher dimensions. In light of this result, we will re-examine some previous works motivated by applications to dislocation theory in materials science. Finally, we will discuss some related results and open questions.
In this note, we prove a formula for the cancellation exponent $k_{v,n}$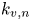 between division polynomials $psi _n$
between division polynomials $psi _n$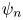 and $phi _n$
and $phi _n$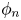 associated with a sequence ${nP}_{nin mathbb {N}}$
associated with a sequence ${nP}_{nin mathbb {N}}$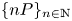 of points on an elliptic curve $E$
of points on an elliptic curve $E$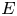 defined over a discrete valuation field $K$
defined over a discrete valuation field $K$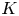 . The formula greatly generalizes the previously known special cases and treats also the case of non-standard Kodaira types for non-perfect residue fields.
. The formula greatly generalizes the previously known special cases and treats also the case of non-standard Kodaira types for non-perfect residue fields.
In the present paper we deal with a quasi-linear elliptic equation depending on a sublinear nonlinearity involving the gradient. We prove the existence of a nontrivial nodal solution employing the theory of invariant sets of descending flow together with sub-supersolution techniques, gradient regularity arguments, strong comparison principle for the $p$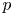 -Laplace operator. The same conclusion is obtained for an eigenvalue problem under a different set of assumptions.
-Laplace operator. The same conclusion is obtained for an eigenvalue problem under a different set of assumptions.

