We define duality triples and duality pairs in compactly generated triangulated categories and investigate their properties. This enables us to give an elementary way to determine whether a class is closed under pure subobjects, pure quotients and pure extensions, as well as providing a way to show the existence of approximations. One key ingredient is a new characterization of phantom maps. We then introduce an axiomatic form of Auslander–Gruson–Jensen duality, from which we define dual definable categories, and show that these coincide with symmetric coproduct closed duality pairs. This framework is ubiquitous, encompassing both algebraic triangulated categories and stable homotopy theories. Accordingly, we provide many applications in both settings, with a particular emphasis on silting theory and stratified tensor-triangulated categories.
The Choquard equation is a partial differential equation that has gained significant interest and attention in recent decades. It is a nonlinear equation that combines elements of both the Laplace and Schrödinger operators, and it arises frequently in the study of numerous physical phenomena, from condensed matter physics to nonlinear optics.
In particular, the steady states of the Choquard equation were thoroughly investigated using a variational functional acting on the wave functions.
In this article, we introduce a dual formulation for the variational functional in terms of the potential induced by the wave function, and use it to explore the existence of steady states of a multi-state version the Choquard equation in critical and sub-critical cases.
In this paper, we consider the following PDE-ODE system modelling cancer invasion with slow diffusion and ECM remodelling,[ begin{cases} u_t=Delta u^m-chinablacdot(unabla v)-xinablacdot(unablaomega)+mu u(1-u-omega), v_t=Delta v+u-v, omega_t={-}vomega+eta omega(1-u-omega). end{cases} ]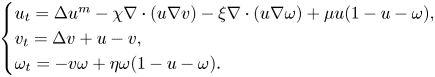
For the special case $eta =0$
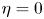, fruitful results have been achieved since Tao and Winkler's work in 2011. However, there is no any progress for the general case $eta >0$
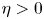in the past ten years. In this paper, we analysed some commonly used research methods when $eta =0$
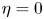, and found that these methods are completely unsuitable for situations where $eta >0$
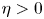. By introducing some new forms of functionals, we reconstruct the relationship between the haptotactic term and the nonlinear diffusion term, and ultimately prove the global existence of weak solutions. This result improves and perfects a series of works previously presented in the literature.
In this paper, we give necessary and sufficient conditions for the rigidity of the perimeter inequality under Schwarz symmetrization. The term rigidity refers to the situation in which the equality cases are only obtained by translations of the symmetric set. In particular, we prove that the sufficient conditions for rigidity provided in M. Barchiesi, F. Cagnetti and N. Fusco [Stability of the Steiner symmetrization of convex sets. J. Eur. Math. Soc. 15 (2013), 1245-1278.] are also necessary.
京公网安备 11010802042870号
京ICP备2023020795号-1
扫码关注我们
求助内容：
应助结果提醒方式：