Forum of Mathematics Sigma最新文献

Faltings ringed topos, the keystone of Faltings’ approach to p-adic Hodge theory for a smooth variety over a local field, relies on the choice of an integral model, and its good properties depend on the (logarithmic) smoothness of this model. Inspired by Deligne’s approach to classical Hodge theory for singular varieties, we establish a cohomological descent result for the structural sheaf of Faltings topos, which makes it possible to extend Faltings’ approach to any integral model, that is, without any smoothness assumption. An essential ingredient of our proof is a variation of Bhatt–Scholze’s arc-descent of perfectoid rings.

In a recent breakthrough, Dimitrov [Dim] solved the Schinzel–Zassenhaus conjecture. We follow his approach and adapt it to certain dynamical systems arising from polynomials of the form 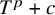$T^p+c$, where p is a prime number and where the orbit of 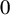$0$ is finite. For example, if 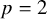$p=2$ and 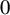$0$ is periodic under 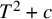$T^2+c$ with 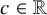$cin mathbb {R}$, we prove a lower bound for the local canonical height of a wandering algebraic integer that is inversely proportional to the field degree. From this, we are able to deduce a lower bound for the canonical height of a wandering point that decays like the inverse square of the field degree. For these f, our method has application to the irreducibility of polynomials. Indeed, say y is preperiodic under f but not periodic. Then any iteration of f minus y is irreducible in 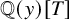$mathbb {Q}(y)[T]$.

We show that, for an arbitrary finite-dimensional quasi-reductive Lie superalgebra over 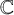${mathbb {C}}$ with a triangular decomposition and a character 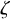$zeta $ of the nilpotent radical, the associated Backelin functor 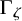$Gamma _zeta $ sends Verma modules to standard Whittaker modules provided the latter exist. As a consequence, this gives a complete solution to the problem of determining the composition factors of the standard Whittaker modules in terms of composition factors of Verma modules in the category ${mathcal {O}}$. In the case of the ortho-symplectic Lie superalgebras, we show that the Backelin functor 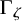$Gamma _zeta $ and its target category, respectively, categorify a q-symmetrizing map and the corresponding q-symmetrized Fock space associated with a quasi-split quantum symmetric pair of type 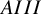$AIII$.

In studying the depth filtration on multiple zeta values, difficulties quickly arise due to a disparity between it and the coradical filtration [9]. In particular, there are additional relations in the depth graded algebra coming from period polynomials of cusp forms for 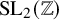$operatorname {mathrm {SL}}_2({mathbb {Z}})$. In contrast, a simple combinatorial filtration, the block filtration [13, 28] is known to agree with the coradical filtration, and so there is no similar defect in the associated graded. However, via an explicit evaluation of 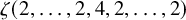$zeta (2,ldots ,2,4,2,ldots ,2)$ as a polynomial in double zeta values, we derive these period polynomial relations as a consequence of an intrinsic symmetry of block graded multiple zeta values in block degree 2. In deriving this evaluation, we find a Galois descent of certain alternating double zeta values to classical double zeta values, which we then apply to give an evaluation of the multiple t values [22] 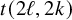$t(2ell ,2k)$ in terms of classical double zeta values.

We prove a stability result of isometric immersions of hypersurfaces in Riemannian manifolds, with respect to 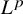$L^p$-perturbations of their fundamental forms: For a manifold 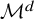${mathcal M}^d$ endowed with a reference metric and a reference shape operator, we show that a sequence of immersions 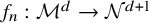$f_n:{mathcal M}^dto {mathcal N}^{d+1}$, whose pullback metrics and shape operators are arbitrary close in 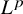$L^p$ to the reference ones, converge to an isometric immersion having the reference shape operator. This result is motivated by elasticity theory and generalizes a previous result [AKM22] to a general target manifold 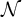${mathcal N}$, removing a constant curvature assumption. The method of proof differs from that in [AKM22]: it extends a Young measure approach that was used in codimension-0 stability results, together with an appropriate relaxation of the energy and a regularity result for immersions satisfying given fundamental forms. In addition, we prove a related quantitative (rather than asymptotic) stability result in the case of Euclidean target, similar to [CMM19] but with no a priori assumed bounds.

We prove that the cohomology rings of the moduli space 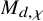$M_{d,chi }$ of one-dimensional sheaves on the projective plane are not isomorphic for general different choices of the Euler characteristics. This stands in contrast to the 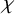$chi $-independence of the Betti numbers of these moduli spaces. As a corollary, we deduce that 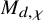$M_{d,chi }$ are topologically different unless they are related by obvious symmetries, strengthening a previous result of Woolf distinguishing them as algebraic varieties.

We prove that all smooth Fano threefolds in the families 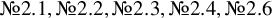and 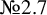are K-stable, and we also prove that smooth Fano threefolds in the family 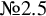that satisfy one very explicit generality condition are K-stable.

The aim of this paper is to study supersoluble skew braces, a class of skew braces that encompasses all finite skew braces of square-free order. It turns out that finite supersoluble skew braces have Sylow towers and that in an arbitrary supersoluble skew brace B many relevant skew brace-theoretical properties are easier to identify: For example, a centrally nilpotent ideal of B is B-centrally nilpotent, a fact that simplifies the computational search for the Fitting ideal; also, B has finite multipermutational level if and only if 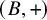$(B,+)$ is nilpotent.

Given a finite presentation of the structure skew brace 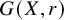$G(X,r)$ associated with a finite nondegenerate solution of the Yang–Baxter equation (YBE), there is an algorithm that decides if 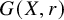$G(X,r)$ is supersoluble or not. Moreover, supersoluble skew braces are examples of almost polycyclic skew braces, so they give rise to solutions of the YBE on which one can algorithmically work on.