We prove a decomposition theorem for the nef cone of smooth fiber products over curves, subject to the necessary condition that their Néron–Severi space decomposes. We apply it to describe the nef cone of so-called Schoen varieties, which are the higher-dimensional analogues of the Calabi–Yau threefolds constructed by Schoen. Schoen varieties give rise to Calabi–Yau pairs, and in each dimension at least three, there exist Schoen varieties with nonpolyhedral nef cone. We prove the Kawamata–Morrison–Totaro cone conjecture for the nef cones of Schoen varieties, which generalizes the work by Grassi and Morrison.
We provide a fine description of the weak limit of sequences of regular axisymmetric maps with equibounded neo-Hookean energy, under the assumption that they have finite surface energy. We prove that these weak limits have a dipole structure, showing that the singular map described by Conti and De Lellis is generic in some sense. On this map, we provide the explicit relaxation of the neo-Hookean energy. We also make a link with Cartesian currents showing that the candidate for the relaxation we obtained presents strong similarities with the relaxed energy in the context of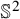 
$mathbb {S}^2$-valued harmonic maps.
We investigate an inverse boundary value problem of determination of a nonlinear law for reaction-diffusion processes, which are modeled by general form semilinear parabolic equations. We do not assume that any solutions to these equations are known a priori, in which case the problem has a well-known gauge symmetry. We determine, under additional assumptions, the semilinear term up to this symmetry in a time-dependent anisotropic case modeled on Riemannian manifolds, and for partial data measurements on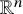 
${mathbb R}^n$.
Moreover, we present cases where it is possible to exploit the nonlinear interaction to break the gauge symmetry. This leads to full determination results of the nonlinear term. As an application, we show that it is possible to give a full resolution to classes of inverse source problems of determining a source term and nonlinear terms simultaneously. This is in strict contrast to inverse source problems for corresponding linear equations, which always have the gauge symmetry. We also consider a Carleman estimate with boundary terms based on intrinsic properties of parabolic equations.
We give a variant of Artin algebraization along closed subschemes and closed substacks. Our main application is the existence of étale, smooth or syntomic neighborhoods of closed subschemes and closed substacks. In particular, we prove local structure theorems for stacks and their derived counterparts and the existence of henselizations along linearly fundamental closed substacks. These results establish the existence of Ferrand pushouts, which answers positively a question of Temkin–Tyomkin.
京公网安备 11010802042870号
京ICP备2023020795号-1
扫码关注我们
求助内容：
应助结果提醒方式：