In this paper, we define two types of strongly decomposable positivity, which serve as generalizations of (dual) Nakano positivity and are stronger than the decomposable positivity introduced by S. Finski. We provide the criteria for strongly decomposable positivity of type I and type II and prove that the Schur forms of a strongly decomposable positive vector bundle of type I are weakly positive, while the Schur forms of a strongly decomposable positive vector bundle of type II are positive. These answer a question of Griffiths affirmatively for strongly decomposably positive vector bundles. Consequently, we present an algebraic proof of the positivity of Schur forms for (dual) Nakano positive vector bundles, which was initially proven by S. Finski.
For a finite-type surface 
$mathfrak {S}$, we study a preferred basis for the commutative algebra 
$mathbb {C}[mathscr {R}_{mathrm {SL}_3(mathbb {C})}(mathfrak {S})]$ of regular functions on the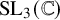 
$mathrm {SL}_3(mathbb {C})$-character variety, introduced by Sikora–Westbury. These basis elements come from the trace functions associated to certain trivalent graphs embedded in the surface 
$mathfrak {S}$. We show that this basis can be naturally indexed by nonnegative integer coordinates, defined by Knutson–Tao rhombus inequalities and modulo 3 congruence conditions. These coordinates are related, by the geometric theory of Fock and Goncharov, to the tropical points at infinity of the dual version of the character variety.
We show that the measure of maximal entropy of every complex Hénon map is exponentially mixing of all orders for Hölder observables. As a consequence, the Central Limit Theorem holds for all Hölder observables.
We use the theory of trianguline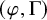 
$(varphi ,Gamma )$-modules over pseudorigid spaces to prove a modularity lifting theorem for certain Galois representations which are trianguline at p, including those with characteristic p coefficients. The use of pseudorigid spaces lets us construct integral models of the trianguline varieties of [BHS17], [Che13] after bounding the slope, and we carry out a Taylor–Wiles patching argument for families of overconvergent modular forms. This permits us to construct a patched quaternionic eigenvariety and deduce our modularity results.
We introduce Chern classes in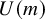 
$U(m)$-equivariant homotopical bordism that refine the Conner–Floyd–Chern classes in the 
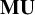$mathbf {MU}$-cohomology of 
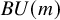$B U(m)$. For products of unitary groups, our Chern classes form regular sequences that generate the augmentation ideal of the equivariant bordism rings. Consequently, the Greenlees–May local homology spectral sequence collapses for products of unitary groups. We use the Chern classes to reprove the 
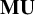$mathbf {MU}$-completion theorem of Greenlees–May and La Vecchia.
We identify the cohomology of the stable classifying space of homotopy automorphisms (relative to an embedded disk) of connected sums of 
${mathrm {S}^{k}} times {mathrm {S}^{l}}$, where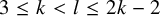 
$3 le k < l le 2k - 2$. The result is expressed in terms of Lie graph complex homology.
Let G be a permutation group on a finite set 
$Omega $. The base size of G is the minimal size of a subset of 
$Omega $ with trivial pointwise stabiliser in G. In this paper, we extend earlier work of Fawcett by determining the precise base size of every finite primitive permutation group of diagonal type. In particular, this is the first family of primitive groups arising in the O’Nan–Scott theorem for which the exact base size has been computed in all cases. Our methods also allow us to determine all the primitive groups of diagonal type with a unique regular suborbit.
This paper extends the results of Boij, Eisenbud, Erman, Schreyer and Söderberg on the structure of Betti cones of finitely generated graded modules and finite free complexes over polynomial rings, to all finitely generated graded rings admitting linear Noether normalizations. The key new input is the existence of lim Ulrich sequences of graded modules over such rings.
京公网安备 11010802042870号
京ICP备2023020795号-1
扫码关注我们
求助内容：
应助结果提醒方式：