We consider bond percolation on high-dimensional product graphs  $G=square _{i=1}^tG^{(i)}$, where
$G=square _{i=1}^tG^{(i)}$, where  $square$ denotes the Cartesian product. We call the
$square$ denotes the Cartesian product. We call the  $G^{(i)}$ the base graphs and the product graph
$G^{(i)}$ the base graphs and the product graph  $G$ the host graph. Very recently, Lichev (J. Graph Theory, 99(4):651–670, 2022) showed that, under a mild requirement on the isoperimetric properties of the base graphs, the component structure of the percolated graph
$G$ the host graph. Very recently, Lichev (J. Graph Theory, 99(4):651–670, 2022) showed that, under a mild requirement on the isoperimetric properties of the base graphs, the component structure of the percolated graph  $G_p$ undergoes a phase transition when
$G_p$ undergoes a phase transition when  $p$ is around
$p$ is around  $frac{1}{d}$, where
$frac{1}{d}$, where  $d$ is the average degree of the host graph.
$d$ is the average degree of the host graph.
In the supercritical regime, we strengthen Lichev’s result by showing that the giant component is in fact unique, with all other components of order
We show that many graphs with bounded treewidth can be described as subgraphs of the strong product of a graph with smaller treewidth and a bounded-size complete graph. To this end, define the underlying treewidth of a graph class  $mathcal{G}$ to be the minimum non-negative integer
$mathcal{G}$ to be the minimum non-negative integer  $c$ such that, for some function
$c$ such that, for some function  $f$, for every graph
$f$, for every graph  $G in mathcal{G}$ there is a graph
$G in mathcal{G}$ there is a graph  $H$ with
$H$ with  $textrm{tw}(H) leqslant c$ such that
$textrm{tw}(H) leqslant c$ such that  $G$ is isomorphic to a subgraph of
$G$ is isomorphic to a subgraph of  $H boxtimes K_{f(textrm{tw}(G))}$. We introduce disjointed coverings of graphs and show they determine the underlying treewidth of any graph class. Using this result, we prove that the class of planar graphs has underlying treewidth
$H boxtimes K_{f(textrm{tw}(G))}$. We introduce disjointed coverings of graphs and show they determine the underlying treewidth of any graph class. Using this result, we prove that the class of planar graphs has underlying treewidth
A graph is called 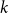 $k$-critical if its chromatic number is
$k$-critical if its chromatic number is 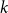 $k$ but every proper subgraph has chromatic number less than
$k$ but every proper subgraph has chromatic number less than 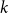 $k$. An old and important problem in graph theory asks to determine the maximum number of edges in an
$k$. An old and important problem in graph theory asks to determine the maximum number of edges in an  $n$-vertex
$n$-vertex 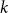 $k$-critical graph. This is widely open for every integer
$k$-critical graph. This is widely open for every integer 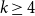 $kgeq 4$. Using a structural characterisation of Greenwell and Lovász and an extremal result of Simonovits, Stiebitz proved in 1987 that for
$kgeq 4$. Using a structural characterisation of Greenwell and Lovász and an extremal result of Simonovits, Stiebitz proved in 1987 that for 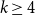 $kgeq 4$ and sufficiently large
$kgeq 4$ and sufficiently large  $n$, this maximum number is less than the number of edges in the
$n$, this maximum number is less than the number of edges in the 

